Rachunek opłacalności inwestycji
„Inwestycja niepodparta rozsądną strategią, to prosta droga do ekonomicznej klęski.”
E. A. Helfert
1. Próg rentowności BEP
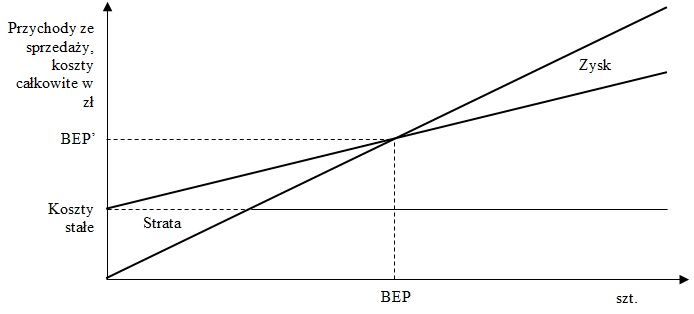
Kalkulacja progu rentowności BEP (z ang.: Break Even Point) jest wykorzystywana do wstępnej oceny projektów inwestycyjnych. Próg rentowności wyznacza granicę, w której realizowane przychody ze sprzedaży pokrywają poniesione koszty. Metoda wyliczenia progu rentowności opiera się na podziale ogółu kosztów na stałe i zmienne, co wymaga usystematyzowania kosztów na podstawie kryterium ich reakcji na zmiany wielkości produkcji. Wyodrębnienie kosztów zmiennych reagujących na zmiany wielkości produkcji i kosztów stałych, niereagujących na te zmiany. W analizie progu rentowności przyjmujemy następujące założenia upraszczające:
- wielkość produkcji w badanym okresie jest dostosowana do wielkości sprzedaży (jest równa wielkości sprzedaży),
- koszty są funkcją wielkości produkcji,
- koszty stałe są jednakowe dla każdej wielkości produkcji,
- jednostkowe koszty zmienne są stałe i w związku z tym całkowite koszty zmienne zmieniają się proporcjonalnie do zmian wielkości produkcji,
- ceny sprzedaży poszczególnych produktów nie ulegają zmianie z upływem czasu i nie zmieniają się również wraz ze zmianą skali produkcji i sprzedaży w całym badanym okresie (przychody ze sprzedaży są więc funkcją liniową ceny sprzedaży i ilości sprzedanych produktów),
- poziom jednostkowych kosztów zmiennych i kosztów stałych pozostaje niezmieniony w całym badanym okresie.
Uwzględniając powyższe można ustalić próg rentowności BEP dla jednego asortymentu produkcji. Próg rentowności BEP może być wyrażony ilościowo lub wartościowo:
BEP ilościowy:
koszty stałe Ks
————————————————————————————————————
jednostkowa cena produktu C [minus] jednostkowy koszty zmienny Kz
BEP′ wartościowy:
koszty stałe Ks
————————————————————————————————————— x C
jednostkowa cena produktu C [minus] jednostkowy koszty zmienny Kz
Schemat 1. Próg rentowności BEP
2. Kalkulacja opłacalności inwestycji dla kapitału własnego KW w punktach
„Musisz robić to, o czym marzysz, nawet gdy się boisz”
Arianna Huffington
1. Przychody ze sprzedaży
2. Koszty operacyjne bez amortyzacji
3. EBITDA
4. Amortyzacja
5. EBIT
6. NOPAT
7. Odsetki od kredytów
8. EBT
9. Podatek dochodowy
10. EAT
11. Aktywa trwałe netto
12. Kapitał obrotowy netto KON
13. Zmiany zapotrzebowania / wycofania kapitału obrotowego netto ⌂KON
14. Wartość rezydualna (resztowa) RV
15. Nakłady kapitałowe IC
a) kapitał własny KW
b) zaciągnięcie kredytów KO
16. Spłaty rat kredytów
17. Zdyskontowane nakłady kapitałowe PVIco
18. Suma zdyskontowanych nakładów kapitałowych ∑ PVIco
19. Oczekiwana stopa zwrotu
20. Współczynnik dyskontowy CO
21. Przepływy pieniężne FCFE
22. Skumulowane saldo przepływów z inwestycji
23. Zdyskontowane przepływy pieniężne FCFEco
24. Suma zdyskontowanych przepływów pieniężnych ∑ FCFEco
25. Stopa zysku
26. Wewnętrzna stopa zwrotu IRR
27. Wartość bieżąca netto NPV
28. Wskaźnik bieżącej wartości netto NPVR
29. Indeks rentowności PI
Objaśnienia do kalkulacji:
- Przychody ze sprzedaży zostały skalkulowane w oparciu o próg rentowności plus procentowy wzrost wartości przychodów w kolejnych latach działalności.
- Koszty operacyjne związane z bieżącym funkcjonowaniem przedsiębiorstwa z wyłączeniem kosztów amortyzacji. Dynamika przyrostu kosztów operacyjnych została dodatnio skorelowana z dynamiką przyrostu przychodów netto ze sprzedaży uwzględniając jednocześnie ewentualną korektę przyrostu tych kosztów o przyjęty współczynnik korygujący.
- EBITDA – wartość wskaźnika EBITDA została wyliczona, jako różnica przychodów netto ze sprzedaży i kosztów operacyjnych bez kosztów amortyzacji.
- Koszty amortyzacji skalkulowane w oparciu o przyjęty plan amortyzacji środków trwałych.
- EBIT – wartość wskaźnika EBIT została wyliczona w wersji uproszczonej (jako zysk z podstawowej działalności operacyjnej), czyli różnica wskaźnika EBITDA i amortyzacji.
- NOPAT – Wartość wskaźnika NOPAT została skalkulowana zgodnie ze wzorem: EBIT x (1 [minus] stawka podatku).
- Odsetki od kredytów zostały skalkulowane w oparciu o plan spłaty kredytów.
- EBT (z ang.: Earnings Before Taxes ) zysk przedsiębiorstwa przed naliczeniem podatku dochodowego – odpowiednik zysku brutto.
- Wartość podatku dochodowego została skalkulowana jako iloraz wartości wskaźnika EBT i stawki podatkowej.
- EAT (z ang.: Earnings After Taxes) zysk przedsiębiorstwa po naliczeniu podatku dochodowego – odpowiednik zysku netto.
- AT (aktywa trwałe netto) są różnicą pomiędzy wartością aktywów trwałych brutto i poziomem amortyzacji.
- Kapitał obrotowy netto KON jest różnicą kapitału stałego (kapitału własnego i długoterminowego obcego) i majątku długookresowego.
- Zmiany zapotrzebowania na kapitał obrotowy netto ⌂KON [minus] kapitał obrotowy netto w poprzednim okresie KONt-1.
- Wartość resztowa RV została skalkulowana jako wartość netto aktywów trwałych AT w ostatnim okresie prognozy.
- Wartość nakładów kapitałowych IC została skalkulowana jako suma nakładów inwestycyjnych na majątek trwały i kapitał obrotowy netto finansowanych z:
a) kapitałów własnych KW,
b) kapitałów obcych KO. - Spłaty rat kredytów zgodne z planem spłaty rat kapitałowych.
- Zdyskontowane nakłady kapitałowe PVIco, to iloraz wartości nakładów kapitałowych IC w danym roku obrotowym i współczynnik dyskonta CO (czynnik dyskonta) przypisany dla danego roku.
- Suma zdyskontowanych nakładów kapitałowych ∑ PVIco (z ang.: Present Value of the Investment) jest sumą ilorazu nakładów IC i współczynnika dyskonta CO.
- Oczekiwana stopa zwrotu dla kapitału własnego KW jest kosztem kapitału własnego.
- Współczynnik dyskontowy CO został wyliczony według wzoru: 1 / (1+ r)n, gdzie: r – oczekiwana stopa zwrotu (w tym przypadku kapitału własnego), n – liczba okresów.
- Wskaźnik wolnych przepływów pieniężnych dla właścicieli FCFE związanych z bieżącym funkcjonowaniem przedsiębiorstwa w kolejnych latach okresu obliczeniowego został skalkulowany jako suma: zysku netto EAT, amortyzacji, zmiany zapotrzebowania / wycofania kapitału obrotowego netto ⌂ KON, wartości rezydualnej RV, spłaty rat kredytów / zaciągnięcia kredytów i nakładów kapitałowych IC.
- Skumulowane saldo przepływów z inwestycji przedstawia okres, w którym poniesione nakłady inwestycyjne zrównują się z planowanymi wpływami. Jest sumą przepływów ∑ FCFE.
- Zdyskontowane przepływy pieniężne FCFEco to iloraz przepływów pieniężnych FCFE i współczynnika dyskontowego CO.
- Suma zdyskontowanych przepływów pieniężnych ∑ FCFEco jest sumą ilorazu przepływów pieniężnych FCFE i współczynnika dyskontowego CO.
- Stopa zysku przedstawia podstawową kalkulację salda przepływów z inwestycji w relacji do poniesionych nakładów.
- Wewnętrzna stopa zwrotu IRR (z ang.: Internal Rate of Return) jest drugą wykorzystywaną w praktyce metodą dyskontową przedstawiającą ocenę projektu inwestycyjnego, przy której obecna wartość wydatków pieniężnych jest równa obecnej wartości wpływów pieniężnych. Przedstawia stopę rentowności planowanej inwestycji, przy której inwestycja jest opłacalna wówczas, gdy wewnętrzna stopa zwrotu IRR jest wyższa od najniższej możliwej do zaakceptowania przez inwestora stopę rentowności przyjętej (w tym przypadku), jako koszt kapitału własnego. Jest to taka stopa procentowa, przy której wartość bieżąca netto NPV jest równa zeru.
- Wartość bieżąca netto NPV (z ang.: Net Present Value) pozwala określić obecną (aktualną) wartość wpływów i wydatków pieniężnych związanych z ocenianym przedsięwzięciem inwestycyjnym, przy oczekiwanej stopie dyskontowej. NPV określa zatem sumę, zdyskontowanych oddzielnie dla każdego roku, przepływów pieniężnych netto, zrealizowanych w całym okresie objętym rachunkiem, przy stałym poziomie stopy procentowej (dyskontowej), ustalonej (w tym przypadku) na poziomie kosztu kapitału własnego. Wartość ta wyraża więc łączną, obecną wartość przepływów pieniężnych netto, które zostaną wygenerowane dzięki realizacji rozpatrywanego przedsięwzięcia inwestycyjnego. Każdy projekt inwestycyjny, którego NPV > 0 jest opłacalny i oznacza, że stopa rentowności tego przedsięwzięcia jest wyższa od stopy określonej i przyjętej do rachunku (w tym wypadku jest to koszt kapitału własnego). Do wyliczenia NPV można wykorzystać równanie:
NPV = ∑ FCFE / (1 + i)t [minus] ∑ IC / (1 + i)t
…..lub, w przypadku, gdy całość nakładów jest ponoszona w okresie t = 0:
NPV = ∑ FCFE / (1 + i)t [minus] IC
…..Gdzie:
…..FCFE – przepływy pieniężne netto związane z bieżącym funkcjonowaniem przedsiębiorstwa,
…..IC – początkowe nakłady kapitałowe,
…..i – roczna stopa procentowa.
28. Wskaźnik bieżącej wartości netto NPVR (z ang.: Net Present Value Ratio) jest ilorazem wartości bieżącej netto NPV i sumy zdyskontowanych nakładów kapitałowych ∑ PVIco.
29. Indeks rentowności PI (z ang.: Profitability Index) jest ilorazem sumy zdyskontowanych wpływów pieniężnych FCFEco (bez IC) i sumy zdyskontowanych nakładów kapitałowych ∑ PVIco.
3. Kalkulacja opłacalności inwestycji dla kapitału całkowitego KC w punktach
„Sukces najczęściej osiągają ci, którzy nie wiedzą, że porażka jest nieunikniona”
Coco Chanel
1. Przychody ze sprzedaży
2. Koszty operacyjne bez amortyzacji
3. EBITDA
4. Amortyzacja
5. EBIT
6. NOPAT
7. Odsetki
8. EBT
9. Podatek dochodowy
10. EAT
11. Aktywa trwałe netto
12. Kapitał obrotowy netto KON
13. Zmiany zapotrzebowania / wycofania kapitału obrotowego netto ⌂KON
14. Wartość rezydualna (resztowa) RV
15. Nakłady kapitałowe IC
16. Spłaty rat kredytów
17. Zdyskontowane nakłady kapitałowe PVIco
18. Suma zdyskontowanych nakładów kapitałowych ∑ PVIco
19. Oczekiwana stopa zwrotu
20. Współczynnik dyskontowy CO
21. Przepływy pieniężne FCFF
22. Skumulowane saldo przepływów z inwestycji
23. Zdyskontowane przepływy pieniężne FCFFco
24. Suma zdyskontowanych przepływów pieniężnych ∑ FCFFco
25. Stopa zysku
26. Wewnętrzna stopa zwrotu IRR
27. Wartość bieżąca netto NPV
28. Wskaźnik bieżącej wartości netto NPVR
29. Indeks rentowności PI
Objaśnienia do kalkulacji:
- Przychody ze sprzedaży zostały skalkulowane w oparciu o próg rentowności plus procentowy wzrost wartości przychodów w kolejnych latach działalności.
- Koszty operacyjne związane z bieżącym funkcjonowaniem przedsiębiorstwa z wyłączeniem kosztów amortyzacji. Dynamika przyrostu kosztów operacyjnych została dodatnio skorelowana z dynamiką przyrostu przychodów netto ze sprzedaży uwzględniając jednocześnie ewentualną korektę przyrostu tych kosztów o przyjęty współczynnik korygujący.
- EBITDA – wartość wskaźnika EBITDA została wyliczona, jako różnica przychodów netto ze sprzedaży i kosztów operacyjnych bez kosztów amortyzacji.
- Koszty amortyzacji zostały skalkulowane w oparciu o przyjęty plan amortyzacji środków trwałych. Koszty amortyzacji skalkulowane jako koszty niewydatkowe.
- EBIT – wartość wskaźnika EBIT została wyliczona w wersji uproszczonej (jako zysk z podstawowej działalności operacyjnej), czyli różnica wskaźnika EBITDA i amortyzacji.
- NOPAT – Wartość wskaźnika NOPAT została skalkulowana zgodnie ze wzorem: EBIT x (1 [minus] stawka podatku).
- W wariancie kalkulacji inwestycji dla kapitału całkowitego KC nie uwzględnia się kosztów odsetkowych kapitału obcego.
- EBT (z ang.: Earnings Before Taxes ) zysk przedsiębiorstwa przed naliczeniem podatku dochodowego – odpowiednik zysku brutto.
- Wartość podatku dochodowego została skalkulowana jako iloraz wartości wskaźnika EBT i stawki podatkowej.
- EAT (z ang.: Earnings After Taxes) zysk przedsiębiorstwa po naliczeniu podatku dochodowego – odpowiednik zysku netto.
- AT (aktywa trwałe netto) są różnicą pomiędzy wartością aktywów trwałych brutto i poziomem amortyzacji.
- Kapitał obrotowy netto KON jest różnicą kapitału stałego (kapitału własnego i długoterminowego obcego) i majątku długookresowego.
- Zmiany zapotrzebowania na kapitał obrotowy netto ⌂KON [minus] kapitał obrotowy netto w poprzednim okresie KONt-1.
- Wartość resztowa RV została skalkulowana jako wartość netto aktywów trwałych AT w ostatnim okresie prognozy.
- Wartość nakładów kapitałowych IC została skalkulowana jako suma nakładów inwestycyjnych na majątek trwały i kapitał obrotowy netto finansowanych z kapitałów własnych KW.
- W wariancie kalkulacji inwestycji dla kapitału całkowitego KC nie uwzględnia się obcych źródeł zasilania kapitałowego, tj. kredytów i pożyczek.
- Zdyskontowane nakłady kapitałowe PVIco, to iloraz wartości nakładów kapitałowych IC w danym roku obrotowym i współczynnik dyskonta CO (czynnik dyskonta) przypisany dla danego roku.
- Suma zdyskontowanych nakładów kapitałowych ∑ PVIco (z ang.: Present Value of the Investment) jest sumą ilorazu nakładów IC i współczynnika dyskonta CO.
- Oczekiwana stopa zwrotu dla kapitału całkowitego KC jest średnim ważonym kosztem kapitału WACC.
- Współczynnik dyskontowy CO został wyliczony według wzoru: 1 / (1+ r)n, gdzie: r – oczekiwana stopa zwrotu (w tym przypadku koszt kapitału WACC), n – liczba okresów.
- Wskaźnik wolnych przepływów pieniężnych dla wszystkich stron finansujących inwestycję FCFF związanych z bieżącym funkcjonowaniem przedsiębiorstwa w kolejnych latach okresu obliczeniowego został skalkulowany jako suma: zysku NOPAT, amortyzacji, zmiany zapotrzebowania / wycofania kapitału obrotowego netto ⌂ KON, wartości rezydualnej RV.
- Skumulowane saldo przepływów z inwestycji przedstawia okres, w którym poniesione nakłady inwestycyjne zrównują się z planowanymi wpływami. Jest sumą przepływów ∑ FCFF.
- Zdyskontowane przepływy pieniężne FCFFco to iloraz przepływów pieniężnych FCFF i współczynnika dyskontowego CO.
- Suma zdyskontowanych przepływów pieniężnych ∑ FCFFco jest sumą ilorazu przepływów pieniężnych FCFF i współczynnika dyskontowego CO.
- Stopa zysku przedstawia podstawową kalkulację salda przepływów z inwestycji w relacji do poniesionych nakładów.
- Wewnętrzna stopa zwrotu IRR (z ang.: Internal Rate of Return) jest drugą wykorzystywaną w praktyce metodą dyskontową przedstawiającą ocenę projektu inwestycyjnego, przy której obecna wartość wydatków pieniężnych jest równa obecnej wartości wpływów pieniężnych. Przedstawia stopę rentowności planowanej inwestycji, przy której inwestycja jest opłacalna wówczas, gdy wewnętrzna stopa zwrotu IRR jest wyższa od najniższej możliwej do zaakceptowania przez inwestora stopę rentowności przyjętej (w tym przypadku), jako koszt kapitału własnego. Jest to taka stopa procentowa, przy której wartość bieżąca netto NPV jest równa zeru.
- Wartość bieżąca netto NPV (z ang.: Net Present Value) pozwala określić obecną (aktualną) wartość wpływów i wydatków pieniężnych związanych z ocenianym przedsięwzięciem inwestycyjnym, przy oczekiwanej stopie dyskontowej. NPV określa zatem sumę, zdyskontowanych oddzielnie dla każdego roku, przepływów pieniężnych netto, zrealizowanych w całym okresie objętym rachunkiem, przy stałym poziomie stopy procentowej (dyskontowej), ustalonej (w tym przypadku) na poziomie średniego ważonego kosztu kapitału WACC. Wartość ta wyraża więc łączną, obecną wartość przepływów pieniężnych netto, które zostaną wygenerowane dzięki realizacji rozpatrywanego przedsięwzięcia inwestycyjnego. Każdy projekt inwestycyjny, którego NPV > 0 jest opłacalny i oznacza, że stopa rentowności tego przedsięwzięcia jest wyższa od stopy określonej i przyjętej do rachunku (w tym wypadku jest to koszt kapitału WACC). Do wyliczenia NPV można wykorzystać równanie:
NPV = ∑ FCFF / (1 + i)t [minus] ∑ IC / (1 + i)t
…..lub, w przypadku, gdy całość nakładów jest ponoszona w okresie t = 0:
NPV = ∑ FCFF / (1 + i)t [minus] IC
…..Gdzie:
…..FCFF – przepływy pieniężne netto związane z bieżącym funkcjonowaniem przedsiębiorstwa,
…..IC – początkowe nakłady kapitałowe,
…..i – roczna stopa procentowa.
28. Wskaźnik bieżącej wartości netto NPVR (z ang.: Net Present Value Ratio) jest ilorazem wartości bieżącej netto NPV i sumy zdyskontowanych nakładów kapitałowych ∑ PVIco.
29. Indeks rentowności PI (z ang.: Profitability Index) jest ilorazem sumy zdyskontowanych wpływów pieniężnych FCFFco (bez IC) i sumy zdyskontowanych nakładów kapitałowych ∑ PVIco.
—
Praktyczne zastosowanie opisanych obliczeń można zobaczyć w załączonej przykładowej kalkulacji opłacalności projektu inwestycyjnego dla kapitału całkowitego i dla kapitału własnego w spółce „Przykład” S.A. – zobacz
—
Uwaga
Wszystkie treści zawarte w niniejszej witrynie mają wyłącznie charakter informacyjny. A wszelkie decyzje podjęte na podstawie tych treści podejmowane będą wyłącznie na odpowiedzialność Użytkownika. Przed przystąpieniem do użytkowania zapoznaj się z Regulaminem.
Będę wdzięczny za wszelkie komentarze, a zwłaszcza krytyczne uwagi i sugestie Użytkowników dotyczące treści zawartych w niniejszej witrynie. Mam świadomość pewnego stopnia ich ogólności i niedoskonałości, lecz żywię głęboką nadzieję, że spotkam się ze zrozumieniem i życzliwością Użytkowników, których pozytywna reakcja jest źródłem mojej największej satysfakcji.
Bibliografia
Opracowano na podstawie: M. Sierpińska, T. Jachna, Metody podejmowania decyzji finansowych, PWN Warszawa 2007, s. 466 – 467; 476 -479. Analiza projektów inwestycyjnych w procesie tworzenia wartości przedsiębiorstwa, P. Mielcarz, P. Paszczyk, PWN, Warszawa 2013.
